Симплекс- метод. Простое объяснение — Викиучебник. Причины создания этого учебника. Они написаны крайне заумным языком и доставляют множество страданий всем, кто пытается с их помощью изучить этот метод линейного программирования. Целью данного учебника является создание простого и доступного описания алгоритма симплекс- метода, которое можно понять, что называется, «с ходу». Задача линейного программирования.

Как решить симплекс методом задачу линейного программирования: базисные и оптимальное решения. Варианты симплексных таблиц и . Качественное и подробное решение Вашей задачи симплекс методом. Пример - Табличный симплекс метод. Необходимо решить задачу линейного программирования. Целевая функция: 2x 1+5x2+3x3+8x4 Узнайте больше о том, что такое симплексный метод для решения задач линейного программирования и как он работает. Решайте задачи легко!

Реализация программы для решения симплекс-методом. Симплекс-метод http:// 2 / 28 . А если целевая функция стремиться к min, то мы приводим ее к каноническому виду, где она стремится к max и затем находим решение . Рассмотрено решение задач линейного программирования симплекс методом. Рассмотрена двойственная задача и ее решение . Решить симплекс метод онлайн задачу на нашем сайте абсолютно бесплатно с подробным и понятным решением.

Номер этого элемента определит разрешающий столбец. На втором шаге определяется разрешающая строка. Для этого нужно найти симплекс отношение: в каждой строке элемент последнего столбца делится на соответствующий элемент разрешающего столбца.

Симплексный метод, Формы записи: симплексная таблица, строчечная форма, строковая форма. Алгоритм решения: метод искусственного базиса . Целью данного учебника является создание простого и доступного описания алгоритма симплекс-метода, которое можно понять, что называется, .

Так получается столбец симплекс- отношений. Минимальный элемент в этом столбце и определяет разрешающую строку. Приступаем к построению новой симплекс- таблицы. Метки y и x для разрешающей строки и столбца соответсвенно меняются местами: y.

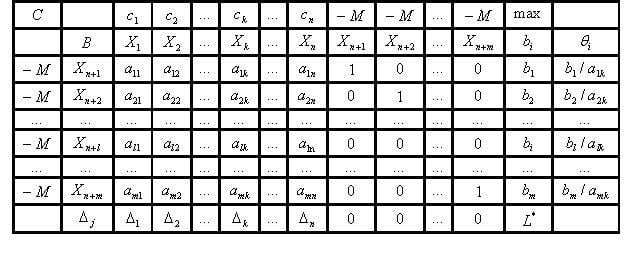
Все элементы разрешающей строки, кроме того, что на пересечении, делим на этот элемент на пересечении. Аудиолекции По Физике далее. Все элементы разрешающего столбца, кроме того, что на пересечении, делим на этот элемент на пересечении и умножаем на . Оно будет находиться в последнем столбце b, его будут обозначать соответствующие метки «x» строк. Подставив найденные x в целевую функцию, находим оптимальное решение.

Решение задач симплекс методом Рассмотрено решение задач линейного программирования симплекс методом. Рассмотрена двойственная задача и ее решение симплекс методом. Дан экономический смысл исходной задачи и переменных двойственной задачи. Рассмотрено решение задачи симплексным М – методом.

Наиболее распространенный вид задач линейного программирования, решаемых симплекс методом, имеет следующий вид: F = c. Тогда получаем систему уравнений: a.

Они определяют пересечение трех плоскостей в 6- ти мерном пространстве. Поскольку линейные функции не имеют локальных экстремумов, то экстремум целевой функции может быть только на границе, определяемой неравенствами x. На этой границе три из 6- ти переменных равны нулю. Значения остальных, которые называются базисом, получаются из решения системы уравнений.

Решение симплекс методом выполняется в два этапа. Выбирается начальный базис. В данном случае это x. Выполняется поиск решения в симплекс таблице.

Если базис не дает оптимального решения, выбирается новый базис, составляется новая симплекс таблица до получения оптимального решения. Экономический смысл задач, решаемых симплекс методом. Здесь, как правило, x. F – общая прибыль; aij – количество затрат i- го сырья на единицу j- го вида продукции; b. Решение двойственной задачи симплекс методом.

Двойственная задача получается из прямой задачи транспонированием матрицы a, меняя b и c местами, а также изменяя знаки неравенств и вида экстремума целевой функции: Z = b. При этом. Zmin = Fmax. Значения y. 1, y. То есть при изменении запасов сырья на .

Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально- денежных ресурсов в количестве b. При этом для продажи 1 группы товаров на 1 тыс. Для продажи 2 и 3 групп товаров на 1 тыс. Прибыль от продажи трех групп товаров на 1 тыс. Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной. Задача N5. 3. К прямой задаче планирования товарооборота, решаемой симплекс методом, составить двойственную задачу линейного программирования.

Установить сопряженные пары переменных прямой и двойственной задачи. Согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров. Решение этой задачи симплекс методом и решение двойственной задачи > > > Решение задач симплекс М – методом.

В некоторых случаях выбрать начальный базис не просто. Например, если имеется дополнительное ограничение x. Тогда неравенство примет вид: x. Поскольку x. 7 . В этом случае, для построения начального базиса, вводят фиктивную переменную x. Если задача имеет решение, то после первых итераций симплекс методом переменная x.

Пример решения задачи симплекс М – методом Найти оптимальные величины производства продукции видов А, Б и В. Затраты сырья на единицу продукции: А – 5, Б – 2, В – 4.

Объем сырья – 2. 00. Затраты оборудования на единицу продукции: А – 4, Б – 5, В – 4. Объем оборудования – 1. Прибыль от реализации единицы продукции: А – 1. Б – 8, В – 1. 2. Критерий – максимум прибыли предприятия. Производство продукции А должно быть не менее 1. Производство продукции Б должно быть не менее 5.

Решение этой задачи симплекс М методом > > >.